Термін (module) у буквальному перекладі з латинської означає «захід». Це було введено в математику англійським ученим Р. Котесом. А німецький математик К. Вейєрштрасс увів у обіг знак модуля – символ, яким це поняття позначається під час написання.

Вконтакте

Вперше це поняття вивчається в математиці за програмою 6 класу середньої школи. Згідно з одним із визначень, модуль - це абсолютне значення дійсного числа. Іншими словами, щоб дізнатись модуль дійсного числа, необхідно відкинути його знак.

Графічно абсолютне значення апозначається як |a|.

Основна відмінна риса цього поняття у тому, що він є неотрицательной величиною.

Числа, які відрізняються один від одного лише знаком, називаються протилежними. Якщо значення позитивне, протилежне йому буде негативним, а нуль є протилежним самому собі.

Геометричне значення

Якщо розглядати поняття модуля з позицій геометрії, він позначатиме відстань, яке вимірюється в одиничних відрізках від початку координат до заданої точки. Це визначення повністю розкриває геометричний сенс досліджуваного терміна.

Графічно можна висловити так: |a| = OA.

Властивості абсолютної величини

Нижче будуть розглянуті всі математичні властивості цього поняття та способи запису у вигляді буквених виразів:

Особливості вирішення рівнянь із модулем

Якщо говорити про розв'язання математичних рівнянь і нерівностей, у яких міститься module, необхідно пам'ятати, що їх вирішення потрібно відкрити цей знак.

Наприклад, якщо знак абсолютної величини містить у собі деякий математичний вираз, перед тим як розкрити модуль, необхідно враховувати діючі математичні визначення.

|А + 5| = А + 5, якщо, А більше або дорівнює нулю.

5-Аякщо А значення менше нуля.

У деяких випадках знак може розкриватися однозначно за будь-яких значень змінної.

Розглянемо ще один приклад. Побудуємо координатну пряму, де відзначимо всі числові значення абсолютної величиною яких буде 5.

Для початку необхідно накреслити координатну пряму, позначити на ній початок координат і встановити розмір одиничного відрізка. Крім того, пряма повинна мати напрямок. Тепер на цій прямій необхідно нанести розмітки, які дорівнюють величині одиничного відрізка.

Таким чином, ми можемо побачити, що на цій координатній прямій будуть дві точки, що цікавлять нас, зі значеннями 5 і -5.

Одна з найскладніших тем для учнів – це розв'язання рівнянь, що містять змінну під знаком модуля. Давайте розберемося для початку з чим це пов'язано? Чому, наприклад, квадратні рівняння більшість дітей клацає як горішки, а з таким далеко не найскладнішим поняттям, як модуль, має стільки проблем?

На мою думку, всі ці складності пов'язані з відсутністю чітко сформульованих правил для вирішення рівнянь із модулем. Так, вирішуючи квадратне рівняння, учень точно знає, що йому потрібно спочатку застосовувати формулу дискримінанта, а потім формули коріння квадратного рівняння. А що робити, якщо на рівнянні зустрівся модуль? Постараємося чітко описати необхідний план дій у разі, коли рівняння містить невідому під знаком модуля. До кожного випадку наведемо кілька прикладів.

Але для початку згадаємо визначення модуля. Отже, модулем числа aназивається саме це число, якщо aневід'ємно і -a, якщо число aменьше нуля. Записати це можна так:

|a| = a, якщо a ≥ 0 та |a| = -a, якщо a< 0

Говорячи про геометричний сенс модуля, слід пам'ятати, що кожному дійсному числу відповідає певна точка на числовій осі - її до оординату. Так ось, модулем або абсолютною величиною числа називається відстань від цієї точки до початку відліку числової осі. Відстань завжди задається позитивним числом. Таким чином, модуль будь-якого негативного числа є позитивним. До речі, навіть на цьому етапі багато учнів починають плутатися. У модулі може стояти будь-яке число, а ось результат застосування модуля завжди число позитивне.

Тепер перейдемо безпосередньо до розв'язання рівнянь.

1. Розглянемо рівняння виду | = с, де с – дійсне число. Це рівняння можна вирішити за допомогою модуля.

Всі дійсні числа розіб'ємо на три групи: ті, що більше за нуль, ті, що менше за нуль, і третя група – це число 0. Запишемо рішення у вигляді схеми:

(±c, якщо з > 0

Якщо | x | = c, то x = (0, якщо с = 0

(немає коріння, якщо з< 0

1) | = 5, т.к. 5> 0, то x = ±5;

2) | = -5 т.к. -5< 0, то уравнение не имеет корней;

3) | = 0 то x = 0.

2. Рівняння виду | f (x) | = b де b > 0. Для вирішення даного рівняння необхідно позбутися модуля. Робимо це: f(x) = b чи f(x) = -b. Тепер необхідно вирішити окремо кожне із отриманих рівнянь. Якщо у вихідному рівнянні b< 0, решений не будет.

1) | x + 2 | = 4, т.к. 4 > 0, то

x + 2 = 4 або x + 2 = -4

2) | x 2 – 5 | = 11, т.к. 11 > 0, то

x 2 - 5 = 11 або x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 немає коріння

3) | x 2 - 5x | = -8, т.к. -8< 0, то уравнение не имеет корней.

3. Рівняння виду | f (x) | = g(x). За змістом модуля таке рівняння матиме рішення, якщо його права частина більша чи дорівнює нулю, тобто. g(x) ≥ 0. Тоді матимемо:

f(x) = g(x)або f(x) = -g(x).

1) | 2x - 1 | = 5x – 10. Це рівняння матиме коріння, якщо 5x – 10 ≥ 0. Саме з цього і починають розв'язання таких рівнянь.

1. О.Д.З. 5x – 10 ≥ 0

2. Рішення:

2x - 1 = 5x - 10 або 2x - 1 = - (5x - 10)

3. Об'єднуємо О.Д.З. та рішення, отримуємо:

Корінь x = 11/7 не підходить за О.Д.З., він менше 2, а x = 3 цій умові задовольняє.

Відповідь: x = 3

2) | x - 1 | = 1 - х 2 .

1. О.Д.З. 1 – x 2 ≥ 0. Розв'яжемо методом інтервалів дану нерівність:

(1 – x)(1 + x) ≥ 0

2. Рішення:

x - 1 = 1 - x 2 або x - 1 = - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 або x = 1 x = 0 або x = 1

3. Об'єднуємо рішення та О.Д.З.:

Підходять лише коріння x = 1 та x = 0.

Відповідь: x=0, x=1.

4. Рівняння виду | f (x) | = | g (x) |. Таке рівняння дорівнює двом наступним рівнянням f(x) = g(x) або f(x) = -g(x).

1) | x 2 - 5x + 7 | = | 2x - 5 |. Це рівняння рівносильне двом наступним:

x 2 - 5x + 7 = 2x - 5 або x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 або x = 4 x = 2 або x = 1

Відповідь: x = 1, x = 2, x = 3, x = 4.

5. Рівняння, які вирішуються шляхом підстановки (заміни змінної). Даний метод рішення найпростіше пояснити на конкретному прикладі. Так, нехай дано квадратне рівняння з модулем:

x 2 – 6|x| + 5 = 0. За якістю модуля x 2 = |x| 2 , тому рівняння можна переписати так:

|х| 2 - 6 | x | + 5 = 0. Зробимо заміну | = t ≥ 0, тоді матимемо:

t 2 – 6t + 5 = 0. Вирішуючи дане рівняння, отримуємо, що t = 1 або t = 5. Повернімося до заміни:

|х| = 1 чи |x| = 5

x = ±1 x = ± 5

Відповідь: x=-5, x=-1, x=1, x=5.

Розглянемо ще один приклад:

x 2 + | – 2 = 0. За якістю модуля x 2 = |x| 2 , тому

|х| 2+ |x| - 2 = 0. Зробимо заміну | x | = t ≥ 0 тоді:

t 2 + t – 2 = 0. Вирішуючи дане рівняння, отримуємо, t = -2 або t = 1. Повернемося до заміни:

|х| = -2 чи |x| = 1

Немає коріння x = ± 1

Відповідь: x=-1, x=1.

6. Ще один вид рівнянь - рівняння зі "складним" модулем. До таких рівнянь відносяться рівняння, в яких є модулі в модулі. Рівняння цього виду можна вирішувати, застосовуючи властивості модуля.

1) |3 – |x|| = 4. Діятимемо так само, як і в рівняннях другого типу. Т.к. 4 > 0, то отримаємо два рівняння:

3 - | x | = 4 чи 3 – |x| = -4.

Тепер виразимо у кожному рівнянні модуль х, тоді | = -1 чи |x| = 7.

Вирішуємо кожне з отриманих рівнянь. У першому рівнянні немає коріння, т.к. -1< 0, а во втором x = ±7.

Відповідь x=-7, x=7.

2) | 3 + | x + 1 | | = 5. Вирішуємо це рівняння аналогічним чином:

3 + | x + 1 | = 5 чи 3 + |x + 1| = -5

|х + 1| = 2 | x + 1 | = -8

x + 1 = 2 або x + 1 = -2. Немає коріння.

Відповідь: x=-3, x=1.

Існує ще й універсальний метод розв'язання рівнянь із модулем. Це спосіб інтервалів. Але ми його розглянемо надалі.

blog.сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

МБОУ ЗОШ №17 м. Іванова

« Рівняння з модулем»
Методична розробка

Складено

вчителем математики

Лебедєвої Н.В.

20010

Пояснювальна записка

Розділ 1. Вступ

Розділ 2. Основні властивості Розділ 3. Геометрична інтерпретація поняття модуля числа Розділ 4. Графік функції у = | Розділ 5. Умовні позначення

Розділ 2. Розв'язання рівнянь, що містять модуль

Розділ 1.Рівняння виду | F (х) | = m (найпростіші) Розділ 2. Рівняння виду F(|х|) = m Розділ 3. Рівняння виду | F (х) | = G(х) Розділ 4. Рівняння виду | F (х) | = ± F(х) (красиві) Розділ 5. Рівняння виду | F (х) | = | G (х) | Розділ 6. Приклади розв'язання нестандартних рівнянь Розділ 7. Рівняння виду | F (х) | + | G (х) | = 0 Розділ 8. Рівняння виду | а 1 х ± 1 | ± |а 2 х ± 2 | ± …|а n х ± у n | = m Розділ 9. Рівняння, що містять кілька модулів

Глава 3. Приклади розв'язання різних рівнянь із модулем.

Розділ 1. Тригонометричні рівняння Розділ 2. Показові рівняння Розділ 3. Логарифмічні рівняння Розділ 4. Ірраціональні рівняння Розділ 5. Завдання підвищеної складності Відповіді до вправ Список літератури

Пояснювальна записка.

Поняття абсолютної величини (модуля) дійсного числа є одним із суттєвих його характеристик. Це поняття має стала вельми поширеною у різних розділах фізико-математичних і технічних наук. У практиці викладання курсу математики в середній школі відповідно до Програми МО РФ поняття «абсолютна величина числа» зустрічається неодноразово: у 6-му класі вводитиметься визначення модуля, його геометричний зміст; у 8 – м класі формується поняття абсолютної похибки, розглядається вирішення найпростіших рівнянь та нерівностей, що містять модуль, вивчаються властивості арифметичного квадратного кореня; в 11-му класі поняття зустрічається в розділі «Корінь n-ой ступеня».Досвід викладання показує, що учні часто стикаються з труднощами під час вирішення завдань, що вимагають знання даного матеріалу, а нерідко пропускають, не приступаючи до виконання. У текстах екзаменаційних завдань за курс 9-ого та 11-ого класів також включені подібні завдання. Крім того, вимоги, які пред'являють до випускників шкіл ВНЗ, відрізняються, а саме, вищого рівня, ніж вимоги шкільної програми. Для життя в суспільстві дуже важливим є формування математичного стилю мислення, що проявляється в певних розумових навичках. У процесі вирішення завдань із модулями потрібно вміння застосовувати такі прийоми, як узагальнення та конкретизація, аналіз, класифікація та систематизація, аналогія. Вирішення подібних завдань дозволяє перевірити знання основних розділів шкільного курсу, рівень логічного мислення, початкові навички дослідницької діяльності. Ця робота присвячена одному з розділів - вирішення рівнянь, що містять модуль. Вона складається з трьох розділів. У першому розділі вводяться основні поняття та найважливіші теоретичні викладки. У другому розділі пропонуються дев'ять основних типів рівнянь, що містять модуль, розглядаються методи їх вирішення, розбираються приклади різного рівня складності. У третьому розділі пропонуються складніші і нестандартні рівняння (тригонометричні, показові, логарифмічні та ірраціональні). До кожного типу рівнянь є вправи для самостійного вирішення (відповіді та вказівки додаються). Основне призначення даної роботи - це надання методичної допомоги викладачам при підготовці до уроків та при організації факультативних курсів. Матеріал також може бути використаний як навчальний посібник для старшокласників. Завдання, запропоновані в роботі, цікаві і не завжди прості у вирішенні, що дозволяє зробити навчальну мотивацію учнів більш усвідомленою, перевірити свої здібності, підвищити рівень підготовки випускників шкіл до вступу до ВНЗ. Диференційований підбір запропонованих вправ передбачає перехід від репродуктивного рівня засвоєння матеріалу до творчого, і навіть можливість навчити застосовувати свої знання під час вирішення нестандартних завдань.

Розділ 1. Вступ.

Розділ 1. Визначення абсолютної величини .

Визначення : Абсолютною величиною (модулем) дійсного числа аназивається невід'ємне число: аабо -А. Позначення: │ а │ Запис читається так: «модуль числа а» або «абсолютна величина числа а»

│ а якщо а > 0

│а│ = │ 0, якщо а = 0 (1)

│ - а, якщо а
Приклади: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Розкрити модуль виразу:

а) │х - 8│, якщо х > 12 б) │2х + 3│, якщо х ≤ -2 │х – 8│= х – 8 │ 2х + 3│= - 2х – 3

Розділ 2. Основні характеристики.

Розглянемо основні властивості абсолютної величини. Властивість №1: Протилежні числа мають рівні модулі, тобто. │а│=│- а│Покажемо вірність рівності. Запишемо визначення числа – а : │- а│= (2) Порівняємо сукупності (1) та (2). Очевидно, що визначення абсолютних величин чисел аі – азбігаються. Отже, │а│=│- а│
При розгляді наступних властивостей обмежимося їх формулюванням, тому що їх доказ наводиться в Властивість №2: Абсолютна величина суми кінцевого числа дійсних чисел не перевищує суми абсолютних величин доданків: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Властивість №3: Абсолютна величина різниці двох дійсних чисел не перевищує суми їх абсолютних величин: │а - в│ ≤│а│+│в│ Властивість №4: Абсолютна величина твору кінцевого числа дійсних чисел дорівнює добутку абсолютних величин множників: │а · в│=│а│·│в│ Властивість №5: Абсолютна величина частки дійсних чисел дорівнює приватному їх абсолютних величин:

Розділ 3. Геометрична інтерпретація поняття модуля числа.

Кожному дійсному числу можна поставити у відповідність точку на числовій прямій, яка буде геометричним зображенням цього дійсного числа. Кожній точці на числовій прямий відповідає відстань від початку відліку, тобто. довжина відрізка від початку відліку до цієї точки. Ця відстань сприймається завжди як величина неотрицательная. Тому довжина відповідного відрізка і буде геометричною інтерпретацією абсолютної величини цього дійсного числа.

Подана геометрична ілюстрація наочно підтверджує якість №1, тобто. модулі протилежних чисел рівні. Звідси легко розуміється справедливість рівності: │х – а│= │а – х│. Також більш очевидним стає рішення рівняння │х│= m, де m ≥ 0, а саме х 1,2 = ± m. Приклади: 1) │х│= 4 х 1,2 = ± 4 2) │х - 3│= 1
х 1,2 = 2; 4

Розділ 4. Графік функції у = │х│

Область визначення цієї функції все дійсні числа.

Розділ 5. Умовні позначення.

Надалі при розгляді прикладів розв'язання рівнянь будуть використані такі умовні позначення: ( - знак системи [ - знак сукупності При розв'язанні системи рівнянь (нерівностей) знаходиться перетин рішень входять до системи рівнянь (нерівностей). При розв'язанні сукупності рівнянь (нерівностей) знаходиться об'єднання рішень, що входять до сукупності рівнянь (нерівностей).

Глава 2. Розв'язання рівнянь, що містять модуль.

У цьому розділі ми розглянемо способи розв'язання алгебри рівнянь, що містять один або більше модуль.

Розділ 1. Рівняння виду │F(х)│= m

Рівняння цього виду називається найпростішим. Воно має рішення тоді і тільки тоді, коли m ≥ 0. За визначенням модуля, вихідне рівняння рівносильне сукупності двох рівнянь: │ F(х)│=m
Приклади:
№1. Розв'яжіть рівняння: │7х - 2│= 9


Відповідь: х 1 = - 1; х 2 = 1 4 / 7 №2
│х 2 + 3х + 1│= 1

х 2 + 3х + 2 = 0 х 2 +3х = 0 х 1 = -1; х 2 = -2 х · (х + 3) = 0 х 1 = 0; х 2 = -3 Відповідь: сума коренів дорівнює - 2.№3
│х 4 -5х 2 + 2│= 2 х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0 х 2 · (х 2 – 5) = 0 позначимо х 2 = m, m ≥ 0 х = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – обидва значення задовольняють умові m ≥ 0 х 2 = 1 х 2 = 4 х = ± 1 х = ± 2 Відповідь: кількість коренів рівняння 7. Вправи:
№1. Розв'яжіть рівняння та вкажіть суму коренів: │х - 5│= 3 №2 . Розв'яжіть рівняння та вкажіть менший корінь: │х 2 + х│= 0 №3 . Розв'яжіть рівняння та вкажіть більший корінь: │х 2 – 5х + 4│= 4 №4 .Рішіть рівняння та вкажіть цілий корінь: │2х 2 – 7х + 6│= 1 №5 .Рішіть рівняння та вкажіть кількість коренів: │х 4 – 13х 2 + 50│= 14

Розділ 2. Рівняння виду F(│х│) = m

Аргумент функції у лівій частині перебуває під знаком модуля, а права частина залежить від змінної. Розглянемо два способи розв'язання рівнянь даного виду. 1 спосіб:За визначенням абсолютної величини вихідне рівняння рівносильне сукупності двох систем. У кожній з яких накладається умова підмодульне вираз. F(│х│) =m
Оскільки функція F(│х│) – парна по всій області визначення, то коріння рівнянь F(х) = m і F(-х) = m – це пари протилежних чисел. Тому досить вирішити одну із систем (при розгляді прикладів вказаним способом буде наводитися рішення однієї системи). 2 спосіб:Застосування методу запровадження нової змінної. При цьому вводиться позначення │х│= а де а ≥ 0. Даний спосіб менш об'ємний по оформленню.
Приклади: №1 . Розв'яжіть рівняння: 3х 2 – 4│х│= - 1 Скористаємося введенням нової змінної. Позначимо │х│= а, де а ≥ 0. Отримаємо рівняння 3а 2 - 4а + 1 = 0 Д = 16 – 12 = 4 а 1 = 1 а 2 = 1/3 Повертаємось до вихідної змінної: │х│=1 та │х│= 1/3 . Кожне рівняння має два корені. Відповідь: х 1 = 1; х 2 = - 1; х 3 = 1 / 3 ; х 4 = - 1 / 3 . №2. Розв'яжіть рівняння: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2
Знайдемо рішення першої системи сукупності: 4х 2 + 5х – 2 =0 Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8 Зауважимо, що х 2 не задовольняє умову х ≥ 0. Рішенням другий системи буде число, протилежне до значення х 1 . Відповідь: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .№3 . Розв'яжіть рівняння: х 4 – │х│= 0 Позначимо │х│= а, де а ≥ 0. Отримаємо рівняння а 4 – а = 0 а · (а 3 – 1) = 0 а 1 = 0 а 2 = 1 Повертаємось до вихідної змінної: │х│=0 та │х│= 1 х = 0; ± 1 Відповідь: х 1 = 0; х 2 = 1; х 3 = - 1.
Вправи: №6. Розв'яжіть рівняння: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Розв'яжіть рівняння, у відповіді вкажіть кількість коренів: 3х 2 - 7│х│ + 2 = 0 №8 . Розв'яжіть рівняння, у відповіді вкажіть цілі рішення: х 4 + │х│ - 2 = 0

Розділ 3. Рівняння виду │F(х)│ = G(х)

Права частина рівняння даного виду залежить від змінної і, отже, має рішення тоді і лише тоді, коли права частина функція G(х) ≥ 0. Вихідне рівняння можна вирішити двома способами: 1 спосіб:Стандартний, заснований на розкритті модуля, виходячи з його визначення і полягає в рівносильному переході до сукупності двох систем. │ F(х)│ =G(х)

Даний спосіб раціонально використовувати у разі складного виразу для функції G(x) і менш складного – для функції F(х), тому що передбачається вирішення нерівностей з функцією F(х). 2 спосіб:Перебуває у переході до рівносильної системі, у якій накладається умова праву частина. │ F(x)│= G(x)

Даний спосіб зручніше застосовувати, якщо вираз для функції G(х) менш складний, ніж для функції F(х), тому що передбачається розв'язання нерівності G(х) ≥ 0. Крім того, у випадку кількох модулів цей спосіб рекомендується застосовувати другий варіант. Приклади: №1. Розв'яжіть рівняння: │х + 2│= 6 -2х
(1 спосіб) Відповідь: х = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(х + 1)
(2 спосіб) Відповідь: Твір коріння – 3.
№3. Розв'яжіть рівняння, у відповіді вкажіть суму коренів:
│х - 6│= х 2 - 5х + 9

Відповідь: сума коренів дорівнює 4.
Вправи: №9. │х + 4│= - 3х №10. Розв'яжіть рівняння, у відповіді вкажіть число розв'язків: │х 2 + х - 1│= 2х – 1 №11 . Розв'яжіть рівняння, у відповіді вкажіть добуток коріння: │х + 3│= х 2 + х – 6

Розділ 4. Рівняння виду │F(x)│= F(x) та │F(x)│= - F(x)

Рівняння цього виду іноді називають «красивими». Оскільки права частина рівнянь залежить від змінної, рішення існують і тоді, коли права частина неотрицательна. Тому вихідні рівняння рівносильні нерівностям:
│F(x)│= F(x) F(x) ≥ 0 та │F(x)│= - F(x) F(x) Приклади: №1 . Розв'яжіть рівняння, у відповіді вкажіть менший цілий корінь: │5х - 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Відповідь: х = 1№2. Розв'яжіть рівняння, у відповіді вкажіть довжину проміжку: │х 2 - 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Відповідь: довжина проміжку дорівнює 6.№3 . Розв'яжіть рівняння, у відповіді вкажіть число цілих розв'язків: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Відповідь: 4 цілих рішення.№4 . Розв'яжіть рівняння, у відповіді вкажіть найбільший корінь:
│4 – х -
│= 4 – х –
х 2 – 5х + 5 = 0 Д = 5 х 1,2 =
≈ 1,4

Відповідь: х = 3.

Вправи: №12. Розв'яжіть рівняння, у відповіді вкажіть цілий корінь: │х 2 + 6х + 8│= х 2 + 6х + 8 №13. Розв'яжіть рівняння, у відповіді вкажіть число цілих рішень: │13х – х 2 - 36│+ х 2 – 13х + 36 = 0 №14. Розв'яжіть рівняння, у відповіді вкажіть ціле число, що не є коренем рівняння:

Розділ 5. Рівняння виду │F(x)│= │G(x)│

Оскільки обидві частини рівняння неотрицательны, то рішення передбачає розгляд двох випадків: підмодульні вирази рівні чи протилежні за знаком. Отже, вихідне рівняння рівносильне сукупності двох рівнянь: │ F(x)│= │ G(x)│
Приклади: №1. Розв'яжіть рівняння, у відповіді вкажіть цілий корінь: │х + 3│=│2х - 1│
Відповідь: ціле коріння х = 4.№2. Розв'яжіть рівняння: │ х – х 2 - 1│=│2х – 3 – х 2 │
Відповідь: х = 2.№3 . Розв'яжіть рівняння, у відповіді вкажіть добуток коріння:




Корні рівняння 4х2 + 2х - 1 = 0х1,2 = - 1±√5 / 4 Відповідь: добуток коріння дорівнює – 0,25. Вправи: №15 . Розв'яжіть рівняння, у відповіді вкажіть ціле рішення: │х 2 – 3х + 2│= │х 2 + 6х - 1│ №16. Розв'яжіть рівняння, у відповіді вкажіть менший корінь:│5х - 3│=│7 - х│ №17 . Розв'яжіть рівняння, у відповіді вкажіть суму коренів:

Розділ 6. Приклади розв'язання нестандартних рівнянь

У розділі ми розглянемо приклади нестандартних рівнянь, під час вирішення яких абсолютна величина висловлювання розкривається за визначенням. Приклади:

№1. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: х · │х│- 5х – 6 = 0
Відповідь: сума коренів дорівнює 1 №2. . Розв'яжіть рівняння, у відповіді вкажіть менший корінь: х 2 - 4х ·
- 5 = 0
Відповідь: менший корінь х = – 5. №3. Розв'яжіть рівняння:

Відповідь: х = -1. Вправи: №18. Розв'яжіть рівняння та вкажіть суму коренів: х · │3х + 5│= 3х 2 + 4х + 3
№19. Розв'яжіть рівняння: х 2 – 3х =

№20. Розв'яжіть рівняння:

Розділ 7. Рівняння виду │F(x)│+│G(x)│=0

Неважко помітити, що у лівій частині рівняння цього виду сума неотрицательных величин. Отже, вихідне рівняння має рішення тоді і лише тоді, коли обидва доданки одночасно дорівнюють нулю. Рівняння рівносильне системі рівнянь: │ F(x)│+│ G(x)│=0
Приклади: №1 . Розв'яжіть рівняння:
Відповідь: х = 2. №2. Розв'яжіть рівняння: Відповідь: х = 1. Вправи: №21. Розв'яжіть рівняння: №22 . Розв'яжіть рівняння, у відповіді вкажіть суму коренів: №23 . Розв'яжіть рівняння, у відповіді вкажіть кількість рішень:

Розділ 8. Рівняння виду │а 1 х + у 1 │±│а 2 х + у 2 │± … │а n х +в n │= m

Для вирішення рівнянь цього виду застосовується метод інтервалів. Якщо його вирішувати послідовним розкриттям модулів, то отримаємо nсукупностей систем, що дуже громіздко та незручно. Розглянемо метод алгоритму інтервалів: 1). Знайти значення змінної х, При яких кожен модуль дорівнює нулю (нулі підмодульних виразів):
2). Знайдені значення відзначити на числовій прямій, яка розбивається на інтервали (кількість інтервалів відповідно дорівнює n+1 ) 3). Визначити, з яким знаком розкривається кожен модуль кожному з отриманих інтервалів (при оформленні рішення можна використовувати числову пряму, відзначивши у ньому знаки) 4). Вихідне рівняння рівносильне сукупності n+1 систем, у кожному у тому числі вказується приналежність змінної ходному з інтервалів. Приклади: №1 . Розв'яжіть рівняння, у відповіді вкажіть найбільший корінь:
1). Знайдемо нулі підмодульних виразів: х = 2; х = -3 2). Зазначимо знайдені значення на числовій прямій та визначимо, з яким знаком розкривається кожен модуль на отриманих інтервалах:
х – 2 х – 2 х – 2 - - + - 3 2 х 2х + 6 2х + 6 2х + 6 - + + 3)
- немає рішень Рівняння має два корені. Відповідь: максимальний корінь х = 2. №2. Розв'яжіть рівняння, у відповіді вкажіть цілий корінь:
1). Знайдемо нулі підмодульних виразів: х = 1,5; х = - 1 2). Зазначимо знайдені значення на числовій прямій і визначимо, з яким знаком розкривається кожен модуль на отриманих інтервалах: х + 1 х + 1 х + 1 - + +
-1 1,5 х 2х - 3 2х - 3 2х - 3 - - +
3).
Остання система не має рішень, отже, рівняння має два корені. Під час розв'язання рівняння слід звернути увагу на знак «-» перед другим модулем. Відповідь: ціле коріння х = 7. №3. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: 1). Знайдемо нулі підмодульних виразів: х = 5; х = 1; х = - 2 2). Зазначимо знайдені значення на числовій прямій і визначимо, з яким знаком розкривається кожен модуль на отриманих інтервалах: х – 5 х – 5 х – 5 х – 5 - - - +
-2 1 5 х х – 1 х – 1 х – 1 х – 1 - - + + х + 2 х + 2 х + 2 х + 2 - + + +
3).
Рівняння має два корені х = 0 та 2. Відповідь: сума коренів дорівнює 2. №4 . Розв'яжіть рівняння: 1). Знайдемо нулі підмодульних виразів: х = 1; х = 2; х = 3. 2). Визначимо, з яким знаком відкривається кожен модуль отриманих інтервалах. 3).
Об'єднаємо рішення перших трьох систем. Відповідь: ; х = 5.
Вправи: №24. Розв'яжіть рівняння:
№25. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: №26. Розв'яжіть рівняння, у відповіді вкажіть менший корінь: №27. Розв'яжіть рівняння, у відповіді вкажіть більший корінь:

Розділ 9. Рівняння, що містять кілька модулів

Рівняння, що містять кілька модулів, передбачають наявність абсолютних величин у підмодульних виразах. Основний принцип розв'язання рівнянь даного виду – це послідовне розкриття модулів, починаючи із зовнішнього. У результаті рішення застосовуються прийоми, розглянуті розділах №1, №3.

Приклади: №1. Розв'яжіть рівняння:
Відповідь: х = 1; – 11. №2. Розв'яжіть рівняння:
Відповідь: х = 0; 4; - 4. №3. Розв'яжіть рівняння, у відповіді вкажіть добуток коріння:
Відповідь: добуток коріння дорівнює - 8. №4. Розв'яжіть рівняння:
Позначимо рівняння сукупності (1) і (2) та розглянемо рішення кожного з них окремо для зручності оформлення. Так як обидва рівняння містять більше одного модуля, зручніше здійснити рівносильний перехід до сукупностей систем. (1)

(2)


Відповідь:
Вправи: №36. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: 5 │3х-5│ = 25 х №37. Розв'яжіть рівняння, якщо коріння більше одного, у відповіді вкажіть суму коренів: │х + 2│ х – 3х – 10 = 1 №38. Розв'яжіть рівняння: 3 │2х -4│ = 9 │х│ №39. Розв'яжіть рівняння, у відповіді вкажіть кількість коренів на : 2 │ sin х│ = √2 №40 . Розв'яжіть рівняння, у відповіді вкажіть кількість коренів:

Розділ 3. Логарифмічні рівняння.

Перед розв'язанням наступних рівнянь необхідно повторити властивості логарифмів та логарифмічної функції. Приклади: №1. Розв'яжіть рівняння, у відповіді вкажіть добуток коріння: log 2 (х+1) 2 + log 2 │x+1│ = 6 О.Д.З. х+1≠0 х≠ - 1

1 випадок: якщо х ≥ - 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – задовольняє умові х ≥ - 1 2 випадок: якщо х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – задовольняє умовою х - 1
Відповідь: добуток коріння дорівнює - 15.
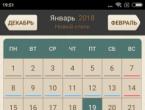
№2. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: lg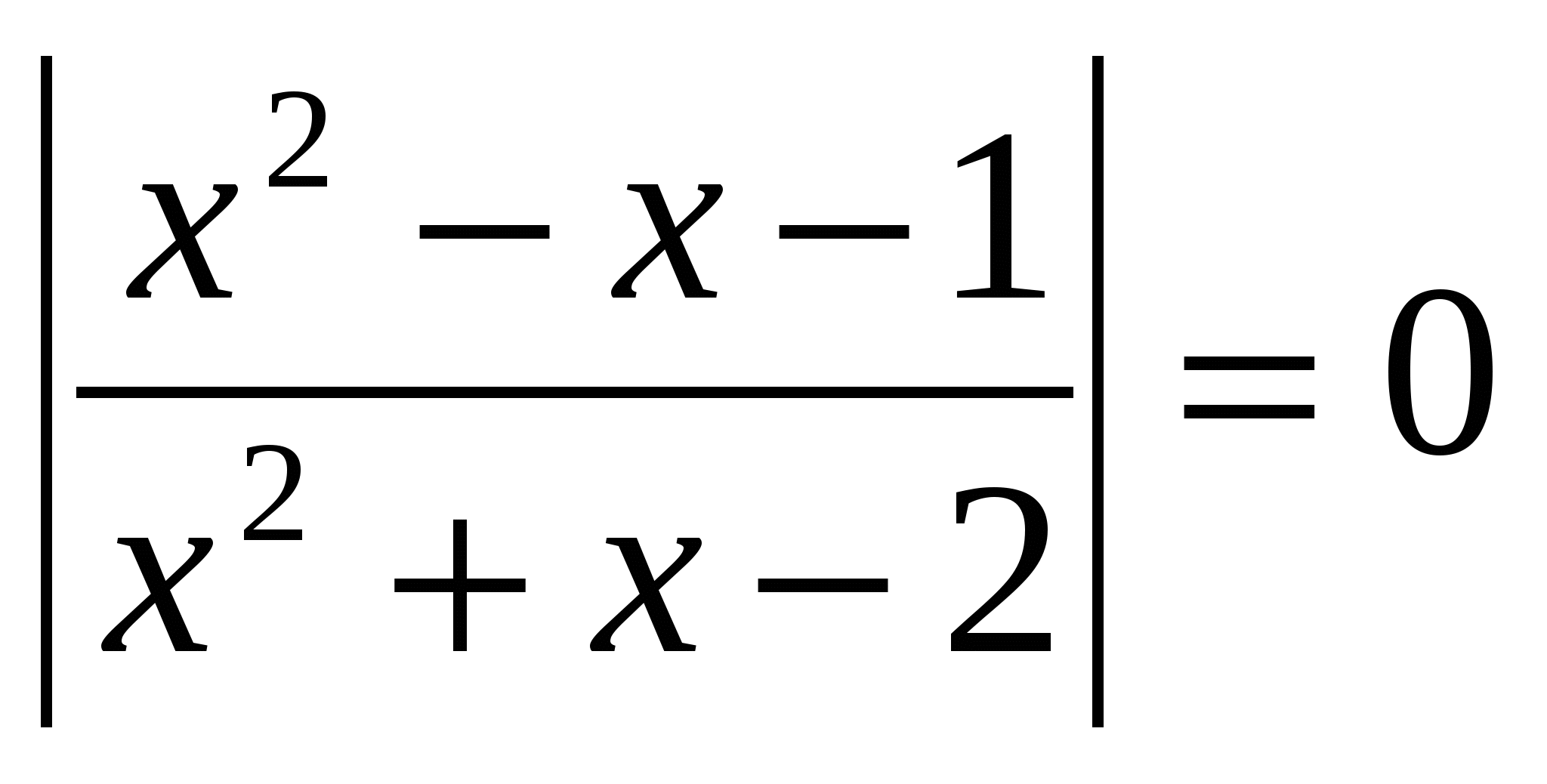
О.Д.З.

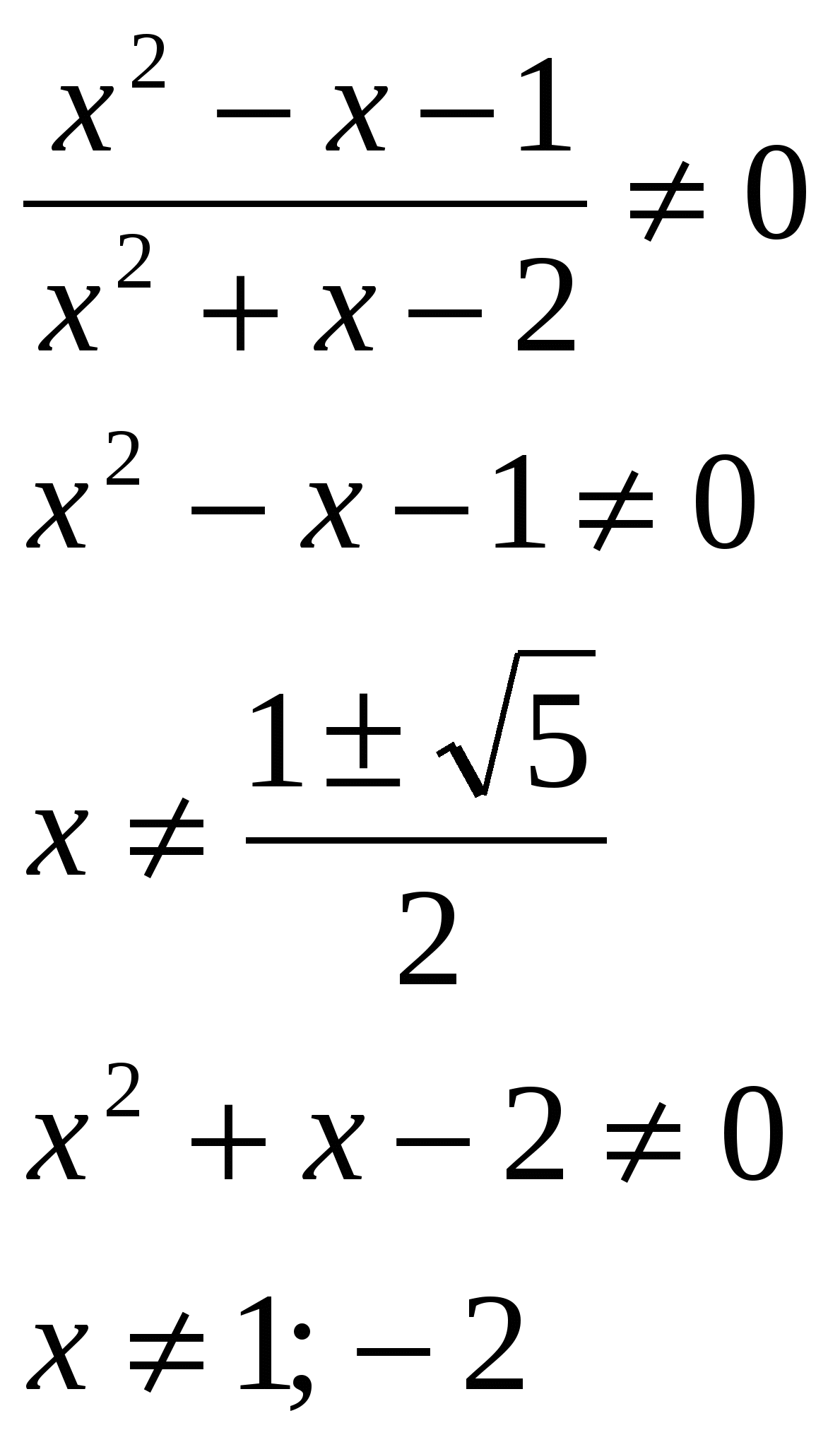
Відповідь: сума коренів дорівнює 0,5.
№3. Розв'яжіть рівняння: log 5
О.Д.З.

Відповідь: х = 9. №4. Розв'яжіть рівняння: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Скористаємося формулою переходу до іншої основи. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Знайдемо нулі підмодульних виразів: х = 25; х = Ці числа ділять область допустимих значень на три інтервали, тому рівняння рівносильне сукупності трьох систем.
Відповідь: )