Головна / Дитяча

Паралелограм у задачах. Як знайти площу паралелограма? Формула для знаходження площі паралелограма

Що таке паралелограм? Паралелограм називається чотирикутник, у якого протилежні сторони попарно паралельні.

1. Площа паралелограма обчислюється за такою формулою:

\[ \LARGE S = a \cdot h_(a)\]

де:
a - сторона паралелограма,
h a - Висота, проведена до цієї сторони.

2. Якщо відомі довжини двох суміжних сторін паралелограма та кут між ними, то площа паралелограма обчислюється за формулою:

\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]

3. Якщо задані діагоналі паралелограма та відомий кут між ними, то площа паралелограма обчислюється за формулою:

\[ \LARGE S = \frac(1)(2) \cdot d_(1) \cdot d_(2) \cdot sin(\alpha) \]

Властивості паралелограма

У паралелограмі протилежні сторони дорівнюють: \(AB = CD \) , \(BC = AD \)

У паралелограмі протилежні кути рівні: \(\angle A = \angle C \) , \(\angle B = \angle D \)

Діагоналі паралелограма в точці перетину діляться навпіл \(AO = OC \) , \(BO = OD \)

Діагональ паралелограма ділить його на два рівні трикутники.

Сума кутів паралелограма, що належать до однієї сторони, дорівнює 180 o:

\(\angle A + \angle B = 180^(o) \), \(\angle B + \angle C = 180^(o)\)

\(\angle C + \angle D = 180^(o) \), \(\angle D + \angle A = 180^(o)\)

Діагоналі та сторони паралелограма пов'язані наступним співвідношенням:

\(d_(1)^(2) + d_(2)^2 = 2a^(2) + 2b^(2) \)

У паралелограмі кут між висотами дорівнює його гострому куту: \(\angle K B H =\angle A \) .

Бісектриси кутів, що належать до однієї сторони паралелограма, взаємно перпендикулярні.

Бісектриси двох протилежних кутів паралелограма паралельні.

Ознаки паралелограма

Чотирьохкутник буде паралелограмом, якщо:

\(AB = CD \) та \(AB || CD \)

\(AB = CD \) та \(BC = AD \)

\(AO = OC \) та \(BO = OD \)

\(\angle A = \angle C \) та \(\angle B = \angle D \)

У вашому браузері вимкнено Javascript.
Щоб розрахувати, необхідно дозволити елементи ActiveX!

При вирішенні завдань на цю тему крім основних властивостей паралелограмаі відповідних формул можна запам'ятати та застосовувати наступне:

  1. Бісектриса внутрішнього кута паралелограма відсікає від нього рівнобедрений трикутник
  2. Бісектриси внутрішніх кутів прилеглі до однієї із сторін паралелограма взаємно перпендикулярні
  3. Бісектриси, що виходять із протилежних внутрішніх кутів паралелограма, паралельні між собою або лежать на одній прямій
  4. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін
  5. Площа паралелограма дорівнює половині твору діагоналей на синус кута між ними.

Розглянемо завдання, під час вирішення яких використовуються дані властивості.

Завдання 1.

Бісектриса кута С паралелограма АВСD перетинає сторону АD у точці М та продовження сторони АВ за точку А у точці Е. Знайдіть периметр паралелограма, якщо АЕ = 4, DМ = 3.

Рішення.

1. Трикутник СМD рівнобедрений. (Властивість 1). Отже, CD = МD = 3 см.

2. Трикутник ЕАМ рівнобедрений.
Отже, АЕ = АМ = 4 див.

3. АD = АМ + МD = 7 див.

4. Периметр АВСD = 20 див.

Відповідь. 20 див.

Завдання 2.

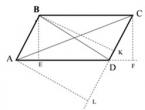
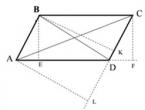
У опуклому чотирикутнику АВСD проведено діагоналі. Відомо, що площа трикутників АВD, АСD, ВСD дорівнює. Доведіть, що цей чотирикутник є паралелограмом.

Рішення.

1. Нехай ВЕ – висота трикутника АВD, СF – висота трикутника АCD. Оскільки за умовою завдання площі трикутників рівні й вони загальне підставу АD, то висоти цих трикутників рівні. ВЕ = СF.

2. ВЕ, СF перпендикулярні до АD. Крапки В і З розташовані з одного боку щодо прямої АD. ВЕ = СF. Отже, пряма ЗС || AD. (*)

3. Нехай АL – висота трикутника АСD, BK – висота трикутника BCD. Оскільки за умовою завдання площі трикутників рівні й вони загальне підставу СD, то висоти цих трикутників рівні. АL=BK.

4. АL та BK перпендикулярні СD. Точки В і А розташовані з одного боку щодо прямої СD. АL=BK. Отже, пряма АВ | CD (**)

5. З умов (*), (**) випливає – АВСD паралелограм.

Відповідь. Доведено. АВСD – паралелограм.

Завдання 3.

На сторонах ВС і CD паралелограма АВСD відзначені точки М і Н відповідно так, що відрізки ВМ і НD перетинаються в точці;<ВМD = 95 о,

Рішення.

1. У трикутнику DОМ<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.

2. У прямокутному трикутнику DНС
(

Тоді<НСD = 30 о. СD: НD = 2: 1
(Оскільки в прямокутному трикутнику катет, що лежить проти кута в 30 о, дорівнює половині гіпотенузи).

Але СD = АВ. Тоді АВ: НD = 2:1.

3. <С = 30 о,

4. <А = <С = 30 о, <В =

Відповідь: АВ: НD = 2: 1,<А = <С = 30 о, <В =

Завдання 4.

Одна з діагоналей паралелограма довжиною 4√6 становить з підставою кут 60 про, а друга діагональ становить з тією ж підставою кут 45 о. Знайти другу діагональ.

Рішення.

1. АТ = 2√6.

2. До трикутника АОD застосуємо теорему синусів.

АТ/sin D = OD/sin А.

2√6/sin 45 про = OD/sin 60 про.

ОD = (2√6sin 60 про) / sin 45 про = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.

Відповідь: 12.

Завдання 5.

У паралелограма зі сторонами 5√2 та 7√2 менший кут між діагоналями дорівнює меншому куту паралелограма. Знайдіть суму довжин діагоналей.

Рішення.

Нехай d 1 , d 2 – діагоналі паралелограма, а кут між діагоналями та менший кут паралелограма дорівнює ф.

1. Порахуємо двома різними
способами його площа.

S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,

S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.

Отримаємо рівність 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф або

2 · 5√2 · 7√2 = d 1 d 2;

2. Використовуючи співвідношення між сторонами та діагоналями паралелограма запишемо рівність

(АВ 2 + АD 2) · 2 = АС 2 + ВD 2.

((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .

d12+d22=296.

3. Складемо систему:

(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140).

Помножимо друге рівняння системи на 2 та складемо з першим.

Отримаємо (d 1 + d 2) 2 = 576. Звідси Id 1 + d 2 I = 24.

Так як d 1 , d 2 - Довжини діагоналей паралелограма, то d 1 + d 2 = 24.

Відповідь: 24.

Завдання 6.

Сторони паралелограма 4 та 6. Гострий кут між діагоналями дорівнює 45 о. Знайдіть площу паралелограма.

Рішення.

1. З трикутника АОВ, використовуючи теорему косінусів, запишемо співвідношення між стороною паралелограма та діагоналями.

АВ 2 = АТ 2 + ВО 2 2 · АТ · ВО · cos АОВ.

4 2 = (d 1 /2) 2 + (d 2 / 2) 2 - 2 · (d 1 / 2) · (d 2 / 2) cos 45 про;

d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.

d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.

2. Аналогічно запишемо співвідношення для трикутника АОD.

Врахуємо, що<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2.

Отримаємо рівняння d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.

3. Маємо систему
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144).

Віднімаючи з другого рівняння перше, отримаємо 2d 1 · d 2 √2 = 80 або

d 1 · d 2 = 80/(2√2) = 20√2

4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.

Примітка:У цьому й попередньому завданні немає потреби, вирішувати повністю систему, передбачаючи те, що у цій задачі для обчислення площі нам необхідний твір діагоналей.

Відповідь: 10.

Завдання 7.

Площа паралелограма дорівнює 96, а його сторони дорівнюють 8 і 15. Знайдіть квадрат меншої діагоналі.

Рішення.

1. S ABCD = AВ · АD · sin ВAD. Зробимо підстановку у формулу.

Отримаємо 96 = 8 · 15 · sin ВAD. Звідси sin ВAD = 4/5.

2. Знайдемо cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.

(4/5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9/25.

За умовою завдання ми знаходимо довжину меншої діагоналі. Діагональ ВD буде меншою, якщо кут ВАD гострий. Тоді cos ВАD = 3/5.

3. З трикутника АВD за теоремою косінусів знайдемо квадрат діагоналі ВD.

ВD 2 = АВ 2 + АD 2 - 2 · АВ · ВD · cos ВАD.

ВD 2 = 8 2 + 15 2 - 2 · 8 · 15 · 3 / 5 = 145.

Відповідь: 145.

Залишились питання? Не знаєте, як розв'язати геометричне завдання?
Щоб отримати допомогу репетитора – зареєструйтесь.
Перший урок – безкоштовно!

сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

Площа геометричної фігури- чисельна характеристика геометричної фігури, що показує розмір цієї фігури (частини поверхні, обмеженої замкнутим контуром цієї фігури). Величина площі виражається числом квадратних одиниць, що укладаються в неї.

Формули площі трикутника

  1. Формула площі трикутника по стороні та висоті
    Площа трикутникадорівнює половині добутку довжини сторони трикутника на довжину проведеної до цієї сторони висоти
  2. Формула площі трикутника по трьох сторонах та радіусу описаного кола
  3. Формула площі трикутника по трьох сторонах і радіусу вписаного кола
    Площа трикутникадорівнює добутку півпериметра трикутника на радіус вписаного кола.
    4. де S - площа трикутника,
    - Довжини сторін трикутника,
    - Висота трикутника,
    - кут між сторонами та,
    - радіус вписаного кола,
    R - радіус описаного кола,

Формули площі квадрата

  1. Формула площі квадрата по довжині сторони
    Площа квадратадорівнює квадрату довжини його боку.
  2. Формула площі квадрата за довжиною діагоналі
    Площа квадратадорівнює половині квадрата довжини його діагоналі.
    S =1 2
    2
    3. де S - площа квадрата,
    - Довжина сторони квадрата,
    - Довжина діагоналі квадрата.

Формула площі прямокутника

    Площа прямокутникадорівнює добутку довжин двох його суміжних сторін

    де S - Площа прямокутника,
    - Довжини сторін прямокутника.

Формули площі паралелограма

  1. Формула площі паралелограма по довжині сторони та висоті
    Площа паралелограма
  2. Формула площі паралелограма з обох боків та кутку між ними
    Площа паралелограмадорівнює добутку довжин його сторін, помноженому на синус кута між ними.

    a · b · sin α

    3. де S - Площа паралелограма,
    - Довжини сторін паралелограма,
    - Довжина висоти паралелограма,
    - Кут між сторонами паралелограма.

Формули площі ромба

  1. Формула площі ромба по довжині сторони та висоті
    Площа ромбудорівнює добутку довжини його сторони та довжини опущеної на цей бік висоти.
  2. Формула площі ромба по довжині сторони та куту
    Площа ромбудорівнює добутку квадрата довжини його сторони та синуса кута між сторонами ромба.
  3. Формула площі ромба за довжинами його діагоналей
    Площа ромбудорівнює половині добутку довжин його діагоналей.
    4. де S - площа ромба,
    - Довжина сторони ромба,
    - Довжина висоти ромба,
    - Кут між сторонами ромба,
    1 2 - довжини діагоналей.

Формули площі трапеції

  1. Формула Герону для трапеції

    Де S - Площа трапеції,
    - Довжини основ трапеції,
    - Довжини бічних сторін трапеції,

Перш ніж дізнатися, як знайти площу паралелограма, нам необхідно згадати, що таке паралелограм і що називається його висотою. Паралелограм – чотирикутник, протилежні сторони якого попарно паралельні (лежать на паралельних прямих). Перпендикуляр, проведений з довільної точки протилежної сторони до прямої, що містить цю сторону, називається висотою паралелограма.

Квадрат, прямокутник і ромб – це окремі випадки паралелограма.

Площа паралелограма позначається як (S).

Формули знаходження площі паралелограма

S=a*h , де а – це основа, h – це висота, яка до підстави.

S=a*b*sinα , де a та b – це основи, а α - кут між основами а та b.

S = p * r, де р - це напівпериметр, r - це радіус кола, яке вписано в паралелограм.

Площа паралелограма, який утворений векторами a та b дорівнює модулю добутку заданих векторів, а саме:

Розглянемо приклад №1: Даний паралелограм, сторона якого дорівнює 7 см, а висота 3 см. Як знайти площу паралелограма, формула для вирішення нам потрібна.

Отже, S= 7x3. S=21. Відповідь: 21 см 2 .

Розглянемо приклад №2: Дано підстави 6 і 7 см, а також дано кут між підставами 60 градусів. Як знайти площу паралелограма? Формула, що використовується для вирішення:

Отже, спочатку знайдемо синус кута. Синус 60 = 0,5, відповідно S = 6 * 7 * 0,5 = 21 Відповідь: 21 см 2 .

Сподіваюся, що ці приклади допоможуть Вам при вирішенні завдань. І пам'ятайте, головне – це знання формул та уважність

Паралелограм – геометрична фігура, що часто зустрічається в задачах курсу геометрії (розділ планіметрії). Ключовими ознаками даного чотирикутника є рівність протилежних кутів та наявність двох пар паралельних протилежних сторін. Окремі випадки паралелограма – ромб, прямокутник, квадрат.

Розрахунок площі даного виду багатокутника може бути проведений декількома способами. Розглянемо кожен із них.

Знайти площу паралелограма, якщо відомі сторона та висота

Для обчислення площі паралелограма можна скористатися значеннями його боку, і навіть довжини висоти, опущеної неї. При цьому отримані дані будуть достовірними як для випадку відомої сторони - підстави фігури, так і якщо у вашому розпорядженні бічна сторона фігури. У такому разі шукана величина буде отримана за формулою:

S = a * h (a) = b * h (b),

  • S – площа, яку слід визначити,
  • a, b – відома (або отримана шляхом обчислень) сторона,
  • h – висота, опущена неї.

Приклад: значення основи паралелограма – 7 см, довжина перпендикуляра, опущеного на нього з протилежної вершини – 3 см.

Рішення: S = a * h (a) = 7 * 3 = 21.

Знайти площу паралелограма, якщо відомі 2 сторони та кут між ними

Розглянемо випадок, коли знаєте величини двох сторін фігури, і навіть градусної міри кута, який вони між собою утворюють. Наданими даними можна скористатися для знаходження площі паралелограма. У цьому випадку вираз-формула матиме такий вигляд:

S = a * c * sinα = a * c * sinβ,

  • a – бічна сторона,
  • с – відома (або отримана шляхом обчислень) підстава,
  • α, β – кути між сторонами a та c.

Приклад: основа паралелограма – 10 см, його бічна сторона на 4 см менша. Тупий кут фігури становить 135 °.

Вирішення: визначаємо значення другої сторони: 10 - 4 = 6 см.

S = a * c * sinα = 10 * 6 * sin135 ° = 60 * sin (90 ° + 45 °) = 60 * cos45 ° = 60 * √2 /2 = 30√2.

Знайти площу паралелограма, якщо відомі діагоналі та кут між ними

Наявність відомих значень діагоналей даного багатокутника, а також кута, який вони утворюють в результаті перетину, дозволяє визначити величину площі фігури.

S = (d1 * d2) / 2 * sinγ,
S = (d1 * d2) / 2 * sinφ,

S – площа, яку слід визначити,
d1, d2 – відомі (або отримані шляхом обчислень) діагоналі,
γ, φ – кути між діагоналями d1 та d2.

Поділитися з друзями:
Схожі публікації