Паралелограм у задачах. Обчислюємо суму кутів і площу паралелограма: властивості та ознаки Знаючи сторони паралелограма знайти його площу

Введіть довжину сторони та висоту до сторони:

Визначення паралелограма

Паралелограм- це чотирикутник, у якому протилежні сторони рівні та паралельні.

Онлайн-калькулятор

Паралелограм має деякі корисні властивості, які спрощують вирішення завдань, пов'язаних з цією фігурою. Наприклад, одне з властивостей у тому, що протилежні кути паралелограма рівні.

Розглянемо кілька методів і формул з наступним рішенням найпростіших прикладів.

Формула площі паралелограма на основі та висоті

Даний спосіб знаходження площі є, напевно, одним з основних і простих, так як він практично ідентичний формулі знаходження площі трикутника за невеликим винятком. Спочатку розберемо узагальнений випадок без використання чисел.

Нехай дано довільний паралелограм з основою a a a, бічною стороною b b bта заввишки h h h, проведеної до нашої основи. Тоді формула для площі цього паралелограма:

S = a ⋅ h S = a \ cdot h S =a ⋅h

A a a- підставу;
h h h- Висота.

Розберемо одне легке завдання, щоб потренуватися у вирішенні типових завдань.

Приклад

Знайти площу паралелограма, в якому відома основа, що дорівнює 10 (див.) і висота, що дорівнює 5 (див.).

Рішення

A = 10 a = 10 a =1 0
h = 5 h = 5 h =5

Підставляємо у нашу формулу. Отримуємо:
S = 10 ⋅ 5 = 50 S=10\cdot 5=50S =1 0 ⋅ 5 = 5 0 (Див. кв.)

Відповідь: 50 (див. кв)

Формула площі паралелограма з обох боків та кутку між ними

В цьому випадку шукана величина знаходиться так:

S = a ⋅ b ⋅ sin ⁡ (α) S=a\cdot b\cdot\sin(\alpha)S =a ⋅b ⋅sin (α)

A, b a, b a, b- Сторони паралелограма;
α \alpha α - Кут між сторонами a a aі b b b.

Тепер розв'яжемо інший приклад і скористаємося вищеописаною формулою.

Приклад

Знайти площу паралелограма якщо відома сторона a a a, що є основою та з довжиною 20 (див.) і периметр p p p, чисельно рівний 100 (див.), кут між суміжними сторонами ( a a aі b b b) дорівнює 30 градусам.

Рішення

A = 20 a = 20 a =2 0
p = 100 p = 100 p =1 0 0
α = 3 0 ∘ \alpha=30^(\circ)α = 3 0 ∘

Для знаходження відповіді нам невідома лише друга сторона цього чотирикутника. Знайдемо її. Периметр паралелограма надається формулою:
p=a+a+b+bp=a+a+b+b p =a +a +b +b
100 = 20 + 20 + b + b 100 = 20+20+b+b1 0 0 = 2 0 + 2 0 + b +b
100 = 40 + 2b 100 = 40 +2b 1 0 0 = 4 0 + 2 b
60 = 2 b 60 = 2b 6 0 = 2 b
b = 30 b = 30 b =3 0

Найскладніше позаду, залишилося тільки підставити наші значення для сторін та кута між ними:
S = 20 ⋅ 30 ⋅ sin ⁡ (3 0 ∘) = 300 S=20\cdot 30\cdot\sin(30^(\circ))=300S =2 0 ⋅ 3 0 ⋅ sin (3 0 ∘ ) = 3 0 0 (Див. кв.)

Відповідь: 300 (див. кв.)

Формула площі паралелограма по діагоналям та розі між ними

S = 1 2 ⋅ D ⋅ d ⋅ sin ⁡ (α) S=\frac(1)(2)\cdot D\cdot d\cdot\sin(\alpha)S =2 1 ​ ⋅ D ⋅d ⋅sin (α)

D D D- велика діагональ;
d d d- мала діагональ;
α \alpha α - Гострий кут між діагоналями.

Приклад

Дано діагоналі паралелограма, рівні 10 (див.) і 5 (див.). Кут між ними 30 градусів. Обчислити його площу.

Рішення

D = 10 D = 10 D =1 0
d = 5 d = 5 d =5
α = 3 0 ∘ \alpha=30^(\circ)α = 3 0 ∘

S = 1 2 ⋅ 10 ⋅ 5 ⋅ sin ⁡ (3 0 ∘) = 12.5 S=\frac(1)(2)\cdot 10 \cdot 5 \cdot\sin(30^(\circ))=12.5S =2 1 ​ ⋅ 1 0 ⋅ 5 ⋅ sin (3 0 ∘ ) = 1 2 . 5 (Див. кв.)

Що таке паралелограм? Паралелограм називається чотирикутник, у якого протилежні сторони попарно паралельні.

1. Площа паралелограма обчислюється за такою формулою:

\[ \LARGE S = a \cdot h_(a)\]

де:
a - сторона паралелограма,
h a - Висота, проведена до цієї сторони.

2. Якщо відомі довжини двох суміжних сторін паралелограма та кут між ними, то площа паралелограма обчислюється за формулою:

\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]

3. Якщо задані діагоналі паралелограма та відомий кут між ними, то площа паралелограма обчислюється за формулою:

\[ \LARGE S = \frac(1)(2) \cdot d_(1) \cdot d_(2) \cdot sin(\alpha) \]

Властивості паралелограма

У паралелограмі протилежні сторони дорівнюють: \(AB = CD \) , \(BC = AD \)

У паралелограмі протилежні кути рівні: \(\angle A = \angle C \) , \(\angle B = \angle D \)

Діагоналі паралелограма в точці перетину діляться навпіл \(AO = OC \) , \(BO = OD \)

Діагональ паралелограма ділить його на два рівні трикутники.

Сума кутів паралелограма, що належать до однієї сторони, дорівнює 180 o:

\(\angle A + \angle B = 180^(o) \), \(\angle B + \angle C = 180^(o)\)

\(\angle C + \angle D = 180^(o) \), \(\angle D + \angle A = 180^(o)\)

Діагоналі та сторони паралелограма пов'язані наступним співвідношенням:

\(d_(1)^(2) + d_(2)^2 = 2a^(2) + 2b^(2) \)

У паралелограмі кут між висотами дорівнює його гострому куту: \(\angle K B H =\angle A \) .

Бісектриси кутів, що належать до однієї сторони паралелограма, взаємно перпендикулярні.

Бісектриси двох протилежних кутів паралелограма паралельні.

Ознаки паралелограма

Чотирьохкутник буде паралелограмом, якщо:

\(AB = CD \) та \(AB || CD \)

\(AB = CD \) та \(BC = AD \)

\(AO = OC \) та \(BO = OD \)

\(\angle A = \angle C \) та \(\angle B = \angle D \)

У вашому браузері вимкнено Javascript.
Щоб розрахувати, необхідно дозволити елементи ActiveX!

Формула для площі паралелограма

Площа паралелограма дорівнює добутку його сторони на висоту, опущену з цього боку.

Доведення

Якщо паралелограм - прямокутник, то рівність виконано за теоремою про площу прямокутника. Далі вважаємо, що кути паралелограма не прямі.

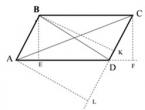
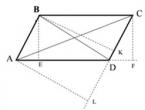
Нехай у паралелограмі $ABCD$ кут $\angle BAD$ гострий і $AD > AB$. Інакше перейменуємо вершини. Тоді висота $BH$ з вершини $B$ на пряму $AD$ падає на бік $AD$, тому що катет $AH$ коротший за гіпотенузу $AB$, а $AB< AD$. Основание $K$ высоты $CK$ из точки $C$ на прямую $AB$ лежит на продолжении отрезка $AD$ за точку $D$, так как угол $\angle BAD$ острый, а значит $\angle CDA$ тупой. Вследствие параллельности прямых $BA$ и $CD$ $\angle BAH = \angle CDK$. В параллелограмме противоположные стороны равны, следовательно, по стороне и двум углам, треугольники $\triangle ABH = \triangle DCK$ равны.

Порівняємо площу паралелограма $ABCD$ і площу прямокутника $HBCK$. Площа паралелограма більша на площу $\triangle ABH$, але менша на на площу $\triangle DCK$. Так як ці трикутники рівні, то їх площі рівні. Значить площа паралелограма дорівнює площі прямокутника зі сторонами довжиною вбік і висоту паралелограма.

Формула для площі паралелограма через сторони та синус

Площа паралелограма дорівнює добутку сусідніх сторін на синус кута між ними.

Доведення

Висота паралелограма $ABCD$, опущена на бік $AB$, дорівнює добутку відрізка $BC$ на синус кута $\angle ABC$. Залишилося застосувати попереднє твердження.

Формула для площі паралелограма через діагоналі

Площа паралелограма дорівнює половині добутку діагоналей на синус кута між ними.

Доведення

Нехай діагоналі паралелограма $ABCD$ перетинаються у точці $O$ під кутом $\alpha$. Тоді $AO=OC$ і $BO=OD$ за якістю паралелограма. Синуси кутів, що в сумі дають $180^\circ$ рівні, $\angle AOB = \angle COD = 180^\circ - \angle BOC = 180^\circ - \angle AOD$. Отже, синуси кутів при перетині діагоналей дорівнюють $\sin\alpha$.

$S_(ABCD)=S_(\triangle AOB) + S_(\triangle BOC) + S_(\triangle COD) + S_(\triangle AOD)$

по аксіомі виміру площі. Застосовуємо формулу площі трикутника $S_(ABC) = \dfrac(1)(2) \cdot AB \cdot BC \sin \angle ABC$ для цих трикутників та кутів при перетині діагоналей. Сторони кожного рівні половина діагоналей, синуси також рівні. Отже, площі всіх чотирьох трикутників дорівнюють $S = \dfrac(1)(2) \cdot \dfrac(AC)(2) \cdot \dfrac(BD)(2) \cdot \sin \alpha = \dfrac(AC \) cdot BD) (8) \ sin \ alpha $. Підсумовуючи все вищесказане, отримуємо

$S_(ABCD) = 4S = 4 \cdot \dfrac(AC \cdot BD)(8) \sin \alpha = \dfrac(AC \cdot BD \cdot \sin \alpha)(2)$

При вирішенні завдань на цю тему крім основних властивостей паралелограмаі відповідних формул можна запам'ятати та застосовувати наступне:

1. Бісектриса внутрішнього кута паралелограма відсікає від нього рівнобедрений трикутник
2. Бісектриси внутрішніх кутів прилеглі до однієї із сторін паралелограма взаємно перпендикулярні
3. Бісектриси, що виходять із протилежних внутрішніх кутів паралелограма, паралельні між собою або лежать на одній прямій
4. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін
5. Площа паралелограма дорівнює половині твору діагоналей на синус кута між ними.

Розглянемо завдання, під час вирішення яких використовуються дані властивості.

Завдання 1.

Бісектриса кута С паралелограма АВСD перетинає сторону АD у точці М та продовження сторони АВ за точку А у точці Е. Знайдіть периметр паралелограма, якщо АЕ = 4, DМ = 3.

Рішення.

1. Трикутник СМD рівнобедрений. (Властивість 1). Отже, CD = МD = 3 см.

2. Трикутник ЕАМ рівнобедрений.
Отже, АЕ = АМ = 4 див.

3. АD = АМ + МD = 7 див.

4. Периметр АВСD = 20 див.

Відповідь. 20 див.

Завдання 2.

У опуклому чотирикутнику АВСD проведено діагоналі. Відомо, що площа трикутників АВD, АСD, ВСD дорівнює. Доведіть, що цей чотирикутник є паралелограмом.

Рішення.

1. Нехай ВЕ – висота трикутника АВD, СF – висота трикутника АCD. Оскільки за умовою завдання площі трикутників рівні й вони загальне підставу АD, то висоти цих трикутників рівні. ВЕ = СF.

2. ВЕ, СF перпендикулярні до АD. Крапки В і З розташовані з одного боку щодо прямої АD. ВЕ = СF. Отже, пряма ЗС || AD. (*)

3. Нехай АL – висота трикутника АСD, BK – висота трикутника BCD. Оскільки за умовою завдання площі трикутників рівні й вони загальне підставу СD, то висоти цих трикутників рівні. АL=BK.

4. АL та BK перпендикулярні СD. Точки В і А розташовані з одного боку щодо прямої СD. АL=BK. Отже, пряма АВ | CD (**)

5. З умов (*), (**) випливає – АВСD паралелограм.

Відповідь. Доведено. АВСD – паралелограм.

Завдання 3.

На сторонах ВС і CD паралелограма АВСD відзначені точки М і Н відповідно так, що відрізки ВМ і НD перетинаються в точці;<ВМD = 95 о,

Рішення.

1. У трикутнику DОМ<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.

2. У прямокутному трикутнику DНС
(

Тоді<НСD = 30 о. СD: НD = 2: 1
(Оскільки в прямокутному трикутнику катет, що лежить проти кута в 30 о, дорівнює половині гіпотенузи).

Але СD = АВ. Тоді АВ: НD = 2:1.

3. <С = 30 о,

4. <А = <С = 30 о, <В =

Відповідь: АВ: НD = 2: 1,<А = <С = 30 о, <В =

Завдання 4.

Одна з діагоналей паралелограма довжиною 4√6 становить з підставою кут 60 про, а друга діагональ становить з тією ж підставою кут 45 о. Знайти другу діагональ.

Рішення.

1. АТ = 2√6.

2. До трикутника АОD застосуємо теорему синусів.

АТ/sin D = OD/sin А.

2√6/sin 45 про = OD/sin 60 про.

ОD = (2√6sin 60 про) / sin 45 про = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.

Відповідь: 12.

Завдання 5.

У паралелограма зі сторонами 5√2 та 7√2 менший кут між діагоналями дорівнює меншому куту паралелограма. Знайдіть суму довжин діагоналей.

Рішення.

Нехай d 1 , d 2 – діагоналі паралелограма, а кут між діагоналями та менший кут паралелограма дорівнює ф.

1. Порахуємо двома різними
способами його площа.

S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,

S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.

Отримаємо рівність 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф або

2 · 5√2 · 7√2 = d 1 d 2;

2. Використовуючи співвідношення між сторонами та діагоналями паралелограма запишемо рівність

(АВ 2 + АD 2) · 2 = АС 2 + ВD 2.

((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .

d12+d22=296.

3. Складемо систему:

(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140).

Помножимо друге рівняння системи на 2 та складемо з першим.

Отримаємо (d 1 + d 2) 2 = 576. Звідси Id 1 + d 2 I = 24.

Так як d 1 , d 2 - Довжини діагоналей паралелограма, то d 1 + d 2 = 24.

Відповідь: 24.

Завдання 6.

Сторони паралелограма 4 та 6. Гострий кут між діагоналями дорівнює 45 о. Знайдіть площу паралелограма.

Рішення.

1. З трикутника АОВ, використовуючи теорему косінусів, запишемо співвідношення між стороною паралелограма та діагоналями.

АВ 2 = АТ 2 + ВО 2 2 · АТ · ВО · cos АОВ.

4 2 = (d 1 /2) 2 + (d 2 / 2) 2 - 2 · (d 1 / 2) · (d 2 / 2) cos 45 про;

d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.

d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.

2. Аналогічно запишемо співвідношення для трикутника АОD.

Врахуємо, що<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2.

Отримаємо рівняння d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.

3. Маємо систему
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144).

Віднімаючи з другого рівняння перше, отримаємо 2d 1 · d 2 √2 = 80 або

d 1 · d 2 = 80/(2√2) = 20√2

4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.

Примітка:У цьому й попередньому завданні немає потреби, вирішувати повністю систему, передбачаючи те, що у цій задачі для обчислення площі нам необхідний твір діагоналей.

Відповідь: 10.

Завдання 7.

Площа паралелограма дорівнює 96, а його сторони дорівнюють 8 і 15. Знайдіть квадрат меншої діагоналі.

Рішення.

1. S ABCD = AВ · АD · sin ВAD. Зробимо підстановку у формулу.

Отримаємо 96 = 8 · 15 · sin ВAD. Звідси sin ВAD = 4/5.

2. Знайдемо cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.

(4/5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9/25.

За умовою завдання ми знаходимо довжину меншої діагоналі. Діагональ ВD буде меншою, якщо кут ВАD гострий. Тоді cos ВАD = 3/5.

3. З трикутника АВD за теоремою косінусів знайдемо квадрат діагоналі ВD.

ВD 2 = АВ 2 + АD 2 - 2 · АВ · ВD · cos ВАD.

ВD 2 = 8 2 + 15 2 - 2 · 8 · 15 · 3 / 5 = 145.

Відповідь: 145.

Залишились питання? Не знаєте, як розв'язати геометричне завдання?
Щоб отримати допомогу репетитора – зареєструйтесь.
Перший урок – безкоштовно!

сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

Паралелограм – геометрична фігура, що часто зустрічається в задачах курсу геометрії (розділ планіметрії). Ключовими ознаками даного чотирикутника є рівність протилежних кутів та наявність двох пар паралельних протилежних сторін. Окремі випадки паралелограма – ромб, прямокутник, квадрат.

Розрахунок площі даного виду багатокутника може бути проведений декількома способами. Розглянемо кожен із них.

Знайти площу паралелограма, якщо відомі сторона та висота

Для обчислення площі паралелограма можна скористатися значеннями його боку, і навіть довжини висоти, опущеної неї. При цьому отримані дані будуть достовірними як для випадку відомої сторони - підстави фігури, так і якщо у вашому розпорядженні бічна сторона фігури. У такому разі шукана величина буде отримана за формулою:

S = a * h (a) = b * h (b),

• S – площа, яку слід визначити,
• a, b – відома (або отримана шляхом обчислень) сторона,
• h – висота, опущена неї.

Приклад: значення основи паралелограма – 7 см, довжина перпендикуляра, опущеного на нього з протилежної вершини – 3 см.

Рішення: S = a * h (a) = 7 * 3 = 21.

Знайти площу паралелограма, якщо відомі 2 сторони та кут між ними

Розглянемо випадок, коли знаєте величини двох сторін фігури, і навіть градусної міри кута, який вони між собою утворюють. Наданими даними можна скористатися для знаходження площі паралелограма. У цьому випадку вираз-формула матиме такий вигляд:

S = a * c * sinα = a * c * sinβ,

• a – бічна сторона,
• с – відома (або отримана шляхом обчислень) підстава,
• α, β – кути між сторонами a та c.

Приклад: основа паралелограма – 10 см, його бічна сторона на 4 см менша. Тупий кут фігури становить 135 °.

Вирішення: визначаємо значення другої сторони: 10 - 4 = 6 см.

S = a * c * sinα = 10 * 6 * sin135 ° = 60 * sin (90 ° + 45 °) = 60 * cos45 ° = 60 * √2 /2 = 30√2.

Знайти площу паралелограма, якщо відомі діагоналі та кут між ними

Наявність відомих значень діагоналей даного багатокутника, а також кута, який вони утворюють в результаті перетину, дозволяє визначити величину площі фігури.

S = (d1 * d2) / 2 * sinγ,
S = (d1 * d2) / 2 * sinφ,

S – площа, яку слід визначити,
d1, d2 – відомі (або отримані шляхом обчислень) діагоналі,
γ, φ – кути між діагоналями d1 та d2.